|

Codage des données
·
Opérateur Booléen
·
Le Binaire
·
Calcul Binaire
·
Le Bit
·
Octet (valeur)
·
Hexadécimal (base 16)
·
Conversion Hexa/Décimal
·
Octal (base 8)
·
Codage des caractères
Opérateurs Booléen
Si une propriété est fausse elle est = 0, si elle est
vraie elle est = 1
Les fonctions de base (ET, OU, OU exclusif et NON)
|
A |
B |
A et B |
|
A |
B |
A ou B |
|
A |
B |
ou X |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
0 |
0 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
1 |
1 |
|
1 |
1 |
1 |
|
1 |
1 |
0 |
Le binaire
Dans les années 30, Claude Shannon démontre qu'à l'aide
d'un interrupteurs fermés pour "vrai" et ouverts pour
"faux" il était possible d'effectuer des opérations
logiques en associant le nombre " 1 " pour "vrai" et "0"
pour "faux".
Ce codage est nommé binaire. C'est avec ce codage que
fonctionnent les ordinateurs. Il consiste à utiliser
deux états (représentés par les chiffres 0 et 1) pour
coder les informations.
|
27 =128 |
26 =64 |
25 =32 |
24 =16 |
23 =8 |
22 =4 |
21 =2 |
20 =1 |
|
|
128 + |
64 + |
32 |
16 |
8 + |
4 = |
2 |
1 |
|
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
= 204 |
Le calcul binaire
Ces tables et les chiffres 0 et 1 permettent de
décomposer les opérations de calcul classique en une
suite d'opérations effectuées au moyen d'opérateurs
booléens. C'est le calcul binaire.
0+0=0 , 0+1=1 , 1+1=0 et je retiens 1 etc...
|
Addition |
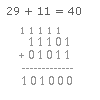 |
|
L'addition se fait avec les mêmes règles
qu'en décimale: On additionner les bits de
poids faibles (A droite) lorsque la somme de
deux bits de mêmes poids dépasse la valeur
de l'unité la plus grande (dans le cas du
binaire:1) on a des retenues, elles sont
reportée sur le bit de poids plus fort
suivant... |
|
La multiplication binaire est très simple |
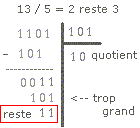
Division |
Soustraction |
|
règle de calcul
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1 |
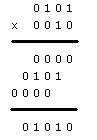 |
 |
 |
| |
|
|
|
Le Bit
|
Le "bit" (contraction des mots anglais
Binary Digit) représente l'unité binaire de
quantité d'information. Il a deux valeurs :
0 ou 1.
Avec un bit il est possible d'obtenir deux
états, soit 1, soit 0.
Avec 2 bits il est possible d'obtenir quatre
états différents (2*2)
Avec 3 bits il est possible d'obtenir huit
états différents (2*2*2 ) etc...
|
|
Avec 2 bits |
|
Avec 3 bits |
|
|
|
|
0 |
0 |
0 |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
|
1 |
1 |
1 |
|
L'octet
L'octet est une unité composée de 8 bits. Il permet de
stocker un caractère, alphanumérique (1 nombre ou 1
lettre). Les anglo-saxons le nomment Byte. Le
regroupement par 8 bits permet une plus grande
lisibilité.
Une unité composée de 16 bits (soit 2 octets) est
appelée mot (en anglais word)
Une unité composée de 32 bits (soit 4 octets) est
appelée double mot (en anglais double word, d'où
l'appellation dword).
Pour un octet, le plus petit nombre est 0 (représenté
par 00000000), le plus grand est 255 (représenté par
11111111), ce qui nous offre 256 possibilités de
valeurs différentes.
Exemple : Un caractère alphanumérique peut être codé par
un mot de 8 bits (la lettre "A" en majuscule du clavier
numérique est =65 en décimal, (table de caractères
ASCII) qui est = 41h en hexadécimal qui est = 01000001
en binaire).
·
Un kilooctet (Ko) = 210
octets = 1024 octets
·
Un mégaoctet (Mo) = 220
octets = 1024 Ko = 1 048 576 octets
·
Un gigaoctet
(Go) = 230 octets = 1024 Mo = 1 073 741 824
octets
·
Un teraoctet
(To) = 240 octets = 1024 Go = 1 099 511 627
776 octets
Hexadécimal (base 16)
L'hexadécimal a 16 valeurs uniques (24 ou 2
x 2 x 2 x 2) pour chacune des colonnes. Cependant nous
n'avons que 10 symboles uniques (0,1,2,3,4,5,6,7,8,9)
pour représenter les chiffres. Les 6 symboles manquants
sont pris dans notre alphabet. 0 1 2 3 4 5 6 7 8 9
A B C D E F
|
Table
de conversion binaire à
hexadécimal |
|
0000 = 0 |
|
0100 = 4 |
|
1000 = 8 |
|
1100 = C |
|
0001 = 1 |
|
0101 = 5 |
|
1001 = 9 |
|
1101 = D |
|
0010 = 2 |
|
0110 = 6 |
|
1010 = A |
|
1110 = E |
|
0011 = 3 |
|
0111 = 7 |
|
1011 = B |
|
1111 = F |
|
|
HEXADECIMAL (base 16)
|
F |
3 |
D |
9 |
|
Colonne |
Opération |
|
| |
| |
| |
└> |
160 |
1 |
1x9 |
|
| |
| |
└ |
─> |
161 |
16 |
16x13 |
|
| |
└ |
─ |
─> |
162 |
256 |
256x3 |
|
└ |
─ |
─ |
─> |
163 |
4096 |
4096x15 |
Ainsi chaque colonne représente une valeur 16 fois plus
grande que la colonne précédente. La colonne suivante
vaut 16 fois plus (1 048 576) et ainsi de suite. Pour
convertir de l'hexadécimal en décimal on multiplie la
colonne par 16 (à la puissance de la position de la
colonne) puis on additionne les valeurs.
Ainsi l'exemple précédent (F3D9), converti en décimal,
donnerait (15 x 4096) + (3 x 256) + (13 x 16) + (9 x 1)
ou la valeur décimale 62 425. Au-delà du chiffre 9, les
lettres représentent des valeurs : A=10, B=11, C=12,
D=13, E=14 et F=15.
Octal (base 8)
Avec 3 bits on peut représenter une valeur comprise
entre 0 et 7, c'est la base 8 (l'octal)
|
Table
de conversion binaire à octal |
|
000 000 = 0 |
|
000 100 = 4 |
|
001 000 = 10 |
|
000 001 = 1 |
|
000 101 = 5 |
|
001 001 = 11 |
|
000 010 = 2 |
|
000 110 = 6 |
|
001 010 = 12 |
|
000 011 = 3 |
|
000 111 = 7 |
|
001 011 = 13 |
|
OCTAL (base 8)
|
1 |
2 |
3 |
4 |
|
Colonne |
Opération |
|
| |
| |
| |
└> |
80 |
1 |
1x4 |
|
| |
| |
└ |
─> |
81 |
8 |
8x3 |
|
| |
└ |
─ |
─> |
82 |
64 |
64x2 |
|
└ |
─ |
─ |
─> |
83 |
512 |
512x1 |
Chaque colonne vaut 8 fois plus que la colonne
précédente (base 8). Pour convertir l'octal en décimal,
vous multipliez la colonne par 8 à la puissance de sa
position. Puis nous additionnons toutes les valeurs.
Dans l'exemple précédent (1 2 3 4), la conversion en
décimal donnerait (1 x 512) + (2 x 64) + (3 x 8) + (4 x
1), ou la valeur décimale 668. La colonne suivante
vaudra 8 fois plus (32768) et ainsi de suite.
Codage des caractères
Le code ASCII (American Standard Code for Information
Interchange)
C'est le système de codage universel. C'est un code à 7
positions, le huitième bit étant réservé a la parité, ce
qui fait 27=128 caractères représentables. Ce
code comprend :
·
des fonctions de commandes
(transmissions de données, tabulations, Retour chariot
...)
·
des symboles de
ponctuations
·
quelques symboles usuels
en informatique (@...)
·
les chiffres
·
les majuscules
·
les minuscules
Certains constructeurs, dont IBM suivis par tous les
fabricants, ont enrichi cette table en utilisant le 8ème
caractère, ce qui double le nombre de caractères
représentables (2 x 128).Les caractères supplémentaires
sont essentiellement :
·
Les caractères accentués
utilisés dans divers langues
·
Quelques symboles
mathématiques
·
Les caractères semi
graphiques qui permettent de réaliser des petits dessins
géométriques.
Il existe un grand nombre de jeux de caractères (pages
de codes)En France, nous utilisons le code multilingue
850 Latin 1
Sur un PC, pour accéder à un caractère, il suffit de
taper ALT et le code ASCII en décimal
Exemple : ALT 64 donnera @.
Les 32 premiers codes et le caractère 127 sont des
caractères de contrôles non imprimables
|
0
1
2
3
4
5
6
7
8
9
10 |
NUL
SOH
STX
ETX
EOT
ENQ
ACK
BEL
BS
HT
LF |
11
12
13
14
15
16
17
18
19
20
21 |
VT
FF
CR
SO
SI
DLE
DC1
DC2
DC3
DC4
NAK |
22
23
24
25
26
27
28
29
30
31
32 |
SYN
ETB
CAN
EM
SUB
ESC
FS
GS
RS
US
space |
33
34
35
36
37
38
39
40
41
42
43 |
!
"
#
$
%
&
'
(
)
*
+ |
44
45
46
47
48
49
50
51
52
53
54 |
,
-
.
/
0
1
2
3
4
5
6 |
55
56
57
58
59
60
61
62
63
64
65 |
7
8
9
:
;
<
=
>
?
@
A |
66
67
68
69
70
71
72
73
74
75
76 |
B
C
D
E
F
G
H
I
J
K
L |
|
77
78
79
80
81
82
83
84
85
86 |
M
N
O
P
Q
R
S
T
U
V |
87
88
89
90
91
92
93
94
95
96 |
W
X
Y
Z
[
\
]
^
-
' |
97
98
99
100
101
102
103
104
105
106 |
a
b
c
d
e
f
g
h
i
j |
107
108
109
110
111
112
113
114
115
116 |
k
l
m
n
o
p
q
r
s
t |
117
118
119
120
121
122
123
124
125
126 |
u
v
w
x
y
z
{
|
}
~ |
127 |
DEL |
|